In my previous post, If it’s not statistically significant, is it useful? (and every grad-school class I taught statistics), I talked about staying within the limits of your data. By that, I mean not making statements that misrepresent what the data can support—basically, keeping it real.
Correlation is not causation
Perhaps the most common example of that is using correlation methods and statistics to make statements that imply causation. My favorite site for worst-case examples of correlations that would make for some curious assumptions of causation is Tyler Vigen’s Spurious Correlation site.
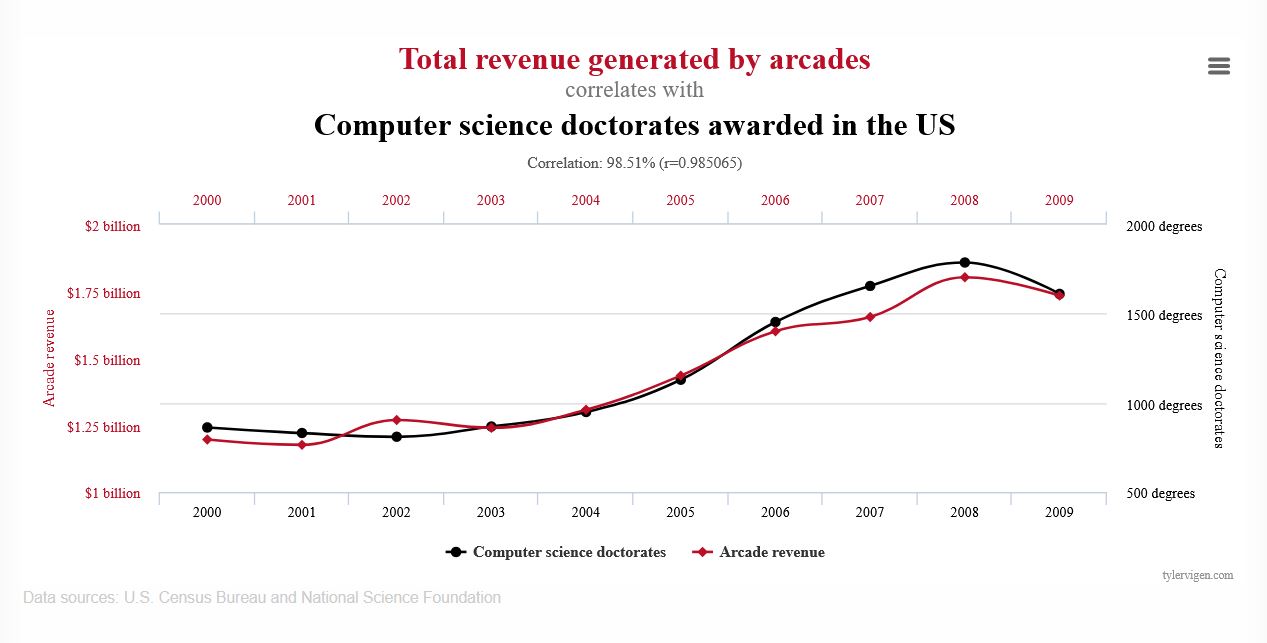
Here’s a fun example. This chart shows that the number of computer science doctorates awarded in the U.S. correlates quite highly with the total revenue generated by arcades from 2000 to 2009.
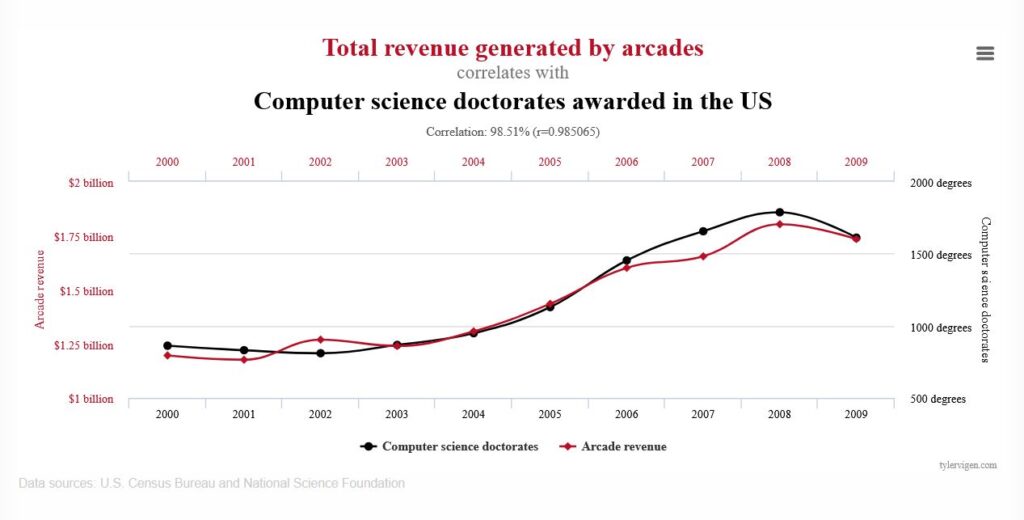
Does this chart say that computer science doctorates caused this revenue? No.
While it’s possible that computer science Ph.D. students contribute a lot of money to arcades or, perhaps, arcades were funding computer science Ph.D. students. The problem is that this chart, or more importantly, this type of comparison, can’t tell us whether either one is true or not. Based on this chart, to say that one of these factors is the cause of the other would be exceeding the limits of this chart.
Describe the data honestly
In my previous post, If it’s not statistically significant, is it useful?, I talk about how the sparse customer feedback in that example couldn’t represent the experience of all the people who looked at a page with a feedback prompt. The 0.03% feedback to page view rate and self-selection of who submitted feedback prevent generalization beyond the responses.
Let’s try an example
Imagine we have a site with the following data from the past year.
- 1,000,000 page views
- A feedback prompt on each page: “Did you find this page helpful?” with the possible answers (responses) being yes or no.
- 120 (40%) yes responses
- 180 (60%) no responses